Menu
Where:
n: number of polygon sides,
b: each length of polygon.
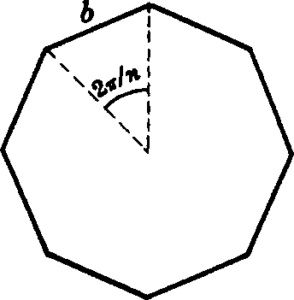
A regular polygon is a polygon in which all sides are of equal length and all angles are of equal measure. The number of sides an n-sided regular polygon has will determine its name. For example, a regular polygon with 3 sides is called a triangle, a regular polygon with 4 sides is called a square, and so on.
- Side length: the length of each side of the polygon
- Apothem: the distance from the center of the polygon to the midpoint of one of its sides
- Perimeter: the total distance around the outside of the polygon, calculated by multiplying the length of one side by the number of sides
- Interior angle: the angle formed inside the polygon at each vertex, calculated by 180*(n-2)/n degrees
- Exterior angle: the angle formed outside the polygon at each vertex, calculated by 360/n degrees
These parameters can be calculated and used to determine various properties and measurements of regular polygons.
Let's consider a regular polygon with n sides. Each side has a length of b units. The total perimeter of the polygon is the sum of all the side lengths.
The perimeter of a regular polygon with n sides can be calculated using the formula:
\text{Perimeter} = n \times b
The interior angles of a regular polygon with n sides can be calculated using the formula:
\text{Interior angle} = \left(180 - \dfrac{360}{n}\right)
The sum of the interior angles of a regular polygon with n sides can be calculated using the formula:
\text{Sum of interior angles} = (n-2) \times 180
The exterior angles of a regular polygon with n sides can be calculated using the formula:
\text{Exterior angle} = \dfrac{360}{n}
The area of a regular polygon with n sides can be calculated using the formula:
\text{Area} = \dfrac{n \times b^2}{4 \times \tan\left(\dfrac{\pi}{n}\right)}
These formulas can be used to calculate the properties of any regular polygon with n sides each of length b. Make sure to substitute the values of n and b into the respective formulas to find the desired property of the regular polygon.
Now, you have a better understanding of the properties of a regular polygon with n sides each of length b. Remember to use the formulas provided to calculate the perimeter, interior and exterior angles, and area of any regular polygon.
Find the interior angle of a regular polygon with 6 sides.
180 - \frac{360}{n}
180 - \frac{360}{6}
180 - 60
120
Determine the exterior angle of a regular polygon with 8 sides.
\frac{360}{n}
\frac{360}{8}
45
Calculate the sum of the interior angles of a regular polygon with 5 sides.
(n-2) \times 180
(5-2) \times 180
3 \times 180
540
Find the measure of each exterior angle of a regular polygon with 12 sides.
\frac{360}{n}
\frac{360}{12}
30
Determine the number of sides of a regular polygon if the measure of each interior angle is 150 degrees.
180 - \frac{360}{n} = 150
\frac{360}{n} = 30
n = 12
1. Find the interior angle of a regular hexagon.
2. Calculate the sum of the interior angles of a regular pentagon.
3. Determine the exterior angle of a regular octagon.
4. Find the measure of each interior angle of a regular heptagon.
5. Calculate the sum of the exterior angles of a regular nonagon.
6. Determine the interior angle of a regular decagon.
7. Find the measure of each exterior angle of a regular dodecagon.
8. Calculate the sum of the interior angles of a regular 20-gon.
9. Determine the exterior angle of a regular 15-gon.
10. Find the measure of each interior angle of a regular 7-gon.
11. Calculate the sum of the exterior angles of a regular 18-gon.
12. Determine the interior angle of a regular 30-gon.
13. Find the measure of each exterior angle of a regular 12-gon.
14. Calculate the sum of the interior angles of a regular 25-gon.
15. Determine the exterior angle of a regular 9-gon.
1. 120^\circ
2. 540^\circ
3. 45^\circ
4. 128.57^\circ
5. 360^\circ
6. 144^\circ
7. 30^\circ
8. 3240^\circ
9. 24^\circ
10. 128.57^\circ
11. 360^\circ
12. 156^\circ
13. 30^\circ
14. 4500^\circ
15. 40^\circ