Where:
h = altitude of the trapezoid
a = length of the parallel side of the trapezoid
b = length of the other parallel side of the trapezoid
θ = incline angle
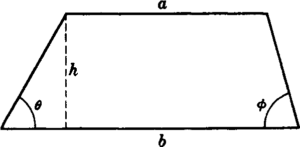
A trapezoid is a quadrilateral with one pair of parallel sides. In this tutorial, we will discuss a trapezoid with altitude h and parallel sides a and b.
Let's denote the incline angle of the trapezoid as θ. The area of the trapezoid can be calculated using the formula:
A = \frac{1}{2} \times h \times (a + b)
This formula is derived from the concept that the area of a trapezoid can be calculated by finding the average of the lengths of the bases and multiplying it by the height.
The perimeter is the sum of the lengths of all sides. In this case, the perimeter P can be calculated as:
P = a + b + 2 \times \sqrt{h^2 + \left(\frac{b - a}{2}\right)^2}
The diagonal of the trapezoid can be calculated using the formula:
D = \sqrt{a^2 + b^2 + 2ab \times \cos(\theta)}
These formulas can be used to calculate the area, perimeter, and diagonal of a trapezoid with altitude h and parallel sides a and b. Practice using these formulas with different values of a, b, h, and θ to deepen your understanding of trapezoids.
1. Bases: In a trapezoid, the parallel sides are called the bases. Let's denote the lengths of the bases as b_1 and b_2.
2. Height: The height (or altitude) of a trapezoid is the perpendicular distance between the two bases. Let's denote the height as h.
3. Sides: The non-parallel sides of a trapezoid are called the legs. The lengths of the legs are usually denoted as a and b.
Find the area of a trapezoid with bases of length 8 cm and 10 cm, and a height of 6 cm.
A = \frac{1}{2}(b_1 + b_2)h
A = \frac{1}{2}(8 + 10)(6)
A = \frac{1}{2}(18)(6)
A = 54 \, cm^2
The area of a trapezoid is 72 square meters. If the bases are 9 meters and 15 meters, find the height.
A = \frac{1}{2}(b_1 + b_2)h
72 = \frac{1}{2}(9 + 15)h
72 = \frac{1}{2}(24)h
72 = 12h
h = 6 \, m
The bases of a trapezoid are of lengths 12 cm and 18 cm. If the area is 120 square centimeters, what is the height?
A = \frac{1}{2}(b_1 + b_2)h
120 = \frac{1}{2}(12 + 18)h
120 = \frac{1}{2}(30)h
120 = 15h
h = 8 \, cm
The area of a trapezoid is 50 square units. If the base lengths are in a ratio of 2:3 and the smaller base is 6 units, find the height.
Let the lengths of the bases be 2x and 3x units.
A = \frac{1}{2}(2x + 3x)h
50 = \frac{1}{2}(5x)h
50 = \frac{5}{2}xh
Given that the smaller base is 6 units:
2x = 6
x = 3
Substitute x into the equation to find h:
50 = \frac{5}{2}(3)h
50 = \frac{15}{2}h
h = \frac{100}{15}
h = \frac{20}{3}
h = \frac{6.\overline{6}}{3}
h = 2.\overline{2} units
The area of a trapezoid is 90 square meters. If the height is 10 meters and the longer base is twice the length of the shorter base, find the lengths of the bases.
Let the lengths of the bases be x and 2x meters.
A = \frac{1}{2}(x + 2x)10
90 = \frac{1}{2}(3x)(10)
90 = 15x
x = 6
So, the lengths of the bases are 6 meters and 12 meters.
1. Find the area of a trapezoid with bases of length 6 and 10, and a height of 4.
2. What is the perimeter of a trapezoid with bases of length 8 and 12, and legs of length 5 and 7?
3. If the area of a trapezoid is 48 square units and its height is 6 units, find the sum of the lengths of its bases.
4. The longer base of a trapezoid is twice the length of the shorter base. If the height is 10 units and the area is 140 square units, find the length of the longer base.
5. Find the area of a trapezoid with bases of length 14 and 18, and a height of 8.
6. What is the perimeter of a trapezoid with bases of length 7 and 11, and legs of length 3 and 5?
7. If the area of a trapezoid is 63 square units and its height is 9 units, find the sum of the lengths of its bases.
8. The longer base of a trapezoid is three times the length of the shorter base. If the height is 12 units and the area is 180 square units, find the length of the longer base.
9. Find the area of a trapezoid with bases of length 12 and 16, and a height of 6.
10. What is the perimeter of a trapezoid with bases of length 9 and 15, and legs of length 4 and 6?
11. If the area of a trapezoid is 72 square units and its height is 8 units, find the sum of the lengths of its bases.
12. The longer base of a trapezoid is four times the length of the shorter base. If the height is 14 units and the area is 224 square units, find the length of the longer base.
13. Find the area of a trapezoid with bases of length 10 and 20, and a height of 5.
14. What is the perimeter of a trapezoid with bases of length 5 and 13, and legs of length 6 and 8?
15. If the area of a trapezoid is 50 square units and its height is 7 units, find the sum of the lengths of its bases.
Answers:
1. 28 square units
2. 32 units
3. 14 units
4. 20 units
5. 136 square units
6. 26 units
7. 18 units
8. 18 units
9. 84 square units
10. 34 units
11. 20 units
12. 28 units
13. 150 square units
14. 32 units
15. 15 units